I. Johdanto
Vesi voi sytyttää kynttilöitä, onko se totta? Se on totta!
Onko totta, että käärmeet pelkäävät realgaria? Se ei pidä paikkaansa!
Tänään keskustelemme seuraavista aiheista:
Häiriöt voivat parantaa mittaustarkkuutta, onko se totta?
Normaalioloissa häiriöt ovat mittauksen luonnollinen vihollinen. Häiriöt heikentävät mittaustarkkuutta. Vaikeissa tapauksissa mittausta ei suoriteta normaalisti. Tästä näkökulmasta häiriöt voivat parantaa mittaustarkkuutta, mikä on väärin!
Mutta onko näin aina? Onko olemassa tilannetta, jossa interferenssi ei vähennä mittaustarkkuutta, vaan pikemminkin parantaa sitä?
Vastaus on kyllä!
2. Häiriösopimus
Yhdessä todellisen tilanteen kanssa teemme seuraavan sopimuksen häiriöstä:
- Häiriöt eivät sisällä tasavirtakomponentteja. Varsinaisessa mittauksessa häiriöt ovat pääasiassa vaihtovirtahäiriöitä, ja tämä oletus on perusteltu.
- Mitatun tasajännitteen arvoon verrattuna interferenssin amplitudi on suhteellisen pieni. Tämä vastaa todellista tilannetta.
- Interferenssi on jaksollinen signaali eli keskiarvo on nolla tietyn ajanjakson sisällä. Tämä ei välttämättä pidä paikkaansa varsinaisessa mittauksessa. Koska interferenssi on kuitenkin yleensä korkeamman taajuuden vaihtovirtasignaali, useimpien häiriöiden kohdalla nollan keskiarvon soveltaminen on järkevää pidemmän ajanjakson aikana.
3. Mittaustarkkuus häiriöiden alaisena
Useimmat sähköiset mittauslaitteet ja mittarit käyttävät nykyään AD-muuntimia, ja niiden mittaustarkkuus liittyy läheisesti AD-muuntimen resoluutioon. Yleisesti ottaen AD-muuntimilla, joilla on korkeampi resoluutio, on myös parempi mittaustarkkuus.
AD-muuntimen resoluutio on kuitenkin aina rajallinen. Olettaen, että AD:n resoluutio on 3 bittiä ja suurin mittausjännite on 8 V, AD-muunnin vastaa asteikkoa, joka on jaettu 8 jakoon, joista jokainen on 1 V. Tämän AD:n mittaustulos on aina kokonaisluku, ja desimaaliosa aina siirretään tai hylätään, kuten tässä artikkelissa oletetaan. Siirtäminen tai hylkääminen aiheuttaa mittausvirheitä. Esimerkiksi 6,3 V on suurempi kuin 6 V ja pienempi kuin 7 V. AD-mittaustulos on 7 V, ja virhe on 0,7 V. Kutsumme tätä virhettä AD-kvantisointivirheeksi.
Analyysin helpottamiseksi oletamme, että asteikolla (AD-muuntimella) ei ole muita mittausvirheitä kuin AD-kvantisointivirhe.
Käytämme nyt kahta identtistä asteikkoa mittaamaan kuvassa 1 esitetyt kaksi tasajännitettä ilman häiriöitä (ihannetilanteessa) ja häiriöiden kanssa.
Kuten kuvassa 1 on esitetty, mitattu todellinen tasajännite on 6,3 V, eikä vasemmanpuoleisessa kuvassa olevalla tasajännitteellä ole häiriöitä ja se on vakioarvoinen. Oikeanpuoleinen kuva näyttää vaihtovirran häiritsemän tasavirran, ja arvossa on tietty vaihtelu. Oikeanpuoleisessa kaaviossa oleva tasajännite on yhtä suuri kuin vasemmanpuoleisessa kaaviossa oleva tasajännite häiriösignaalin poistamisen jälkeen. Kuvassa oleva punainen neliö edustaa AD-muuntimen muunnostulosta.

Ihanteellinen tasajännite ilman häiriöitä
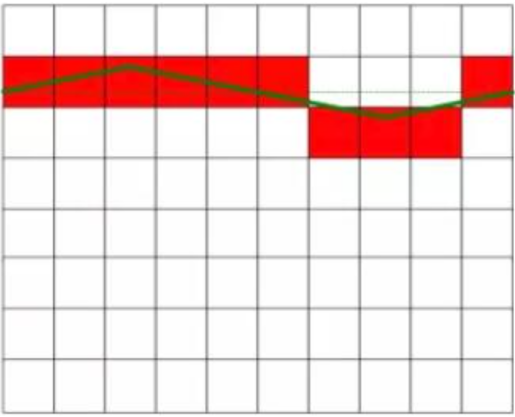
Syötä häiritsevää tasajännitettä, jonka keskiarvo on nolla
Tee 10 tasavirran mittausta yllä olevan kuvan kahdessa tapauksessa ja laske sitten näiden 10 mittauksen keskiarvo.
Ensimmäinen vasemmalla oleva asteikko mitataan 10 kertaa, ja lukemat ovat joka kerta samat. AD-kvantisointivirheen vaikutuksesta jokainen lukema on 7 V. Kymmenen mittauksen keskiarvon laskemisen jälkeen tulos on edelleen 7 V. AD-kvantisointivirhe on 0,7 V ja mittausvirhe on 0,7 V.
Toinen oikeanpuoleinen asteikko on muuttunut dramaattisesti:
Interferenssijännitteen ja amplitudin positiivisen ja negatiivisen eron vuoksi AD-kvantisointivirhe on erilainen eri mittauspisteissä. AD-kvantisointivirheen muuttuessa AD-mittaustulos muuttuu 6 V:n ja 7 V:n välillä. Seitsemän mittauksesta oli 7 V, vain kolme oli 6 V, ja 10 mittauksen keskiarvo oli 6,3 V! Virhe on 0 V!
Itse asiassa mikään virhe ei ole mahdotonta, koska objektiivisessa maailmassa ei ole olemassa ehdotonta 6,3 V:n jännitettä! On kuitenkin olemassa:
Jos häiriöitä ei ole, koska jokainen mittaustulos on sama, virhe pysyy muuttumattomana 10 mittauksen keskiarvon laskemisen jälkeen!
Kun interferenssiä on sopiva määrä, AD-kvantisointivirhe pienenee 10 mittauksen keskiarvon laskemisen jälkeen suuruusluokan! Resoluutio paranee suuruusluokan! Myös mittaustarkkuus paranee suuruusluokan!
Keskeiset kysymykset ovat:
Onko se sama, kun mitattu jännite on muulla arvolla?
Lukijat voivat halutessaan seurata toisen osan interferenssiä koskevaa sopimusta, ilmaista interferenssin numeeristen arvojen sarjana, päällekkäistää interferenssin mitatun jännitteen kanssa ja laskea sitten kunkin pisteen mittaustulokset AD-muuntimen siirtoperiaatteen mukaisesti. Lopuksi he voivat laskea keskiarvon tarkistusta varten, kunhan interferenssiamplitudi voi aiheuttaa lukeman muutoksen AD-kvantisoinnin jälkeen ja näytteenottotaajuus on riittävän korkea (interferenssiamplitudin muutoksilla on siirtymäprosessi, eikä kaksi positiivista ja negatiivista arvoa), ja tarkkuutta on parannettava!
Voidaan todistaa, että niin kauan kuin mitattu jännite ei ole täysin kokonaisluku (sitä ei ole olemassa objektiivimaailmassa), AD-kvantisointivirhettä esiintyy riippumatta siitä, kuinka suuri AD-kvantisointivirhe on. Niin kauan kuin interferenssin amplitudi on suurempi kuin AD-kvantisointivirhe tai suurempi kuin AD:n pienin resoluutio, se aiheuttaa mittaustuloksen muutoksen kahden vierekkäisen arvon välillä. Koska interferenssi on positiivisesti ja negatiivisesti symmetrinen, sen laskun ja kasvun suuruus ja todennäköisyys ovat samat. Siksi, kun todellinen arvo on lähempänä mitä arvoa, minkä arvon esiintymisen todennäköisyys on suurempi, ja se on lähellä mitä arvoa keskiarvon laskemisen jälkeen.
Eli: useiden mittausten keskiarvon (häiriöiden keskiarvo on nolla) on oltava lähempänä häiritsemätöntä mittaustulosta, eli käyttämällä AC-häiriösignaalia, jonka keskiarvo on nolla, ja laskemalla useiden mittausten keskiarvo, voidaan vähentää vastaavia AD-kvantisointivirheitä, parantaa AD-mittausten resoluutiota ja parantaa mittaustarkkuutta!
Julkaisun aika: 13.7.2023




